Projectile motion is a fascinating subject in physics when we are trying to understand the motion of objects that are launched or thrown. The most common acceleration that affects projectile motion is gravity. If a projectile moves with initial velocity in the gravitational field of the earth, the equation
s(t) = (1/2)gt^2 + v_0t
holds, where is the traveled distance at time . Now let’s explore some real-world examples of this equation:
A Magician in a Wooden Chest
Here is an intriguing example of projectile motion that seeks to determine how much time a magician will have to escape after being fired from a wooden chest using a cannon at a certain height.
A magician is locked in a wooden chest and fired straight up from a powerful cannon. We know that the cannon can launch him up to 50 meters high. However, the critical fact is that the magician has a parachute to land safely, but it won’t work if it’s open less than 25 meters from the ground.
Solution 1
Let’s start by determining the time it takes for the magician to fall back to the ground from a height of 50 meters, the maximum height the cannon can launch him. We will do this by using the standard equation of motion.
When the magician lands safely with his parachute, it means he has traveled 50-25=25 meters since the parachute was opened. We can use this fact and the equation below to solve for the time he takes to reach 25 meters:
s(t) = (1/2)gt^2 + v_0t
Firstly, we know that at a height of 50 meters, the vertical velocity is zero since the magician has just left the cannon. Hence the initial velocity . Secondly, we know that when the magician opens his parachute, he has fallen 25 meters. We can substitute these values into the equation to get:
25 = (1/2)(9.8)t^2 /* g=9.8m/s^2 */
Solving for t, we get:
t = sqrt(5) seconds
Therefore, the magician will have about 1.8 seconds to open his parachute before hitting the ground.
Solution 2
This version of the problem seeks to find out how much time the magician will have to escape from the chest if it takes a dummy six seconds to land on the ground.
Here, we know that the distance the dummy fell is what the magician has to travel to escape the chest. We can solve for the maximum height the magician will reach by using the equation:
s(t) = (1/2)gt^2 + v_0t
The initial velocity is zero, while we know that it took the dummy six seconds to hit the ground. We can substitute these values into the equation:
s(6) = (1/2)(9.8)(6^2) /* g=9.8m/s^2 */
Solving for s(6), we get:
s(6) = 176.4m
Therefore, if the cannon launches the magician to a maximum height of 176.4 meters, he will have six seconds to escape from the wooden chest.
A Football Kicker
Another real-world problem that involves projectile motion is a football kicker. Suppose that a football kicker wants to determine the minimum kick velocity to clear the crossbar of a field goal.
We can use projectile motion equations to solve this problem. Assuming that the kicker launches the ball from the ground (initial height, ) at an angle with respect to the horizontal and wants the ball to clear a crossbar of meters, we can solve for the minimum kick velocity using the equation:
This equation comes from equating the maximum height of the ball to the height of the crossbar and solving for the minimum initial velocity. Therefore, the solution is independent of the range of the kick.
A Baseball Pitcher
Suppose a baseball pitcher wants to throw the ball with a minimum velocity to reach the catcher at the same height, but with a greater range.
We can use projectile motion equations to solve this problem by assuming that the catcher is at the same height as the pitcher (initial height, ) and is located at a horizontal distance away from the pitcher. The pitcher wants to throw the ball with the minimum initial velocity possible so that it will land in the catcher’s hand at the same height but has a longer range.
The minimum initial velocity can be found using the equation:
This equation comes from equating the horizontal distance traveled by the ball to the distance between the pitcher and the catcher, solving for the velocity.
A Rocket Launch
A rocket launch is an excellent example of projectile motion in which the object is blasted upward with an initial velocity. Suppose that we want to determine the maximum height that a rocket can reach.
Using projectile motion equations to solve this problem, we can say that the initial velocity is the velocity at which the rocket is launched. We can solve for the maximum height above the launch site using the equation:
h_max = v_0^2 / (2g) /* g=9.8m/s^2 */
Therefore, the maximum height will depend solely on the initial launch velocity of the rocket.
A Stone Ejected from a Volcano
Another fascinating example of projectile motion is a stone ejected from a volcano. Suppose that we want to determine the maximum height that a stone ejected from a volcano can reach.
We can use projectile motion equations to solve this problem. We assume that the initial velocity is the velocity at which the stone is ejected upwards from the volcano. We can solve for the maximum height above the volcano using the equation:
h_max = (v_0^2 / 2g) + h_i /* g=9.8m/s^2 */
Here, represents the initial height of the volcano before the stone is ejected. Therefore, the maximum height will depend on both the initial launch velocity of the stone and the initial height of the volcano.
Conclusion
Projectile motion plays an essential role in physics as it helps us determine the motion of objects that are thrown or launched in the air. The examples presented here show how real-world problems can be solved by using projectile equations.
Real World Examples For Projectile Thrown Upwards Or Downwards
Projectile motion is a fascinating subject in physics when we are trying to understand the motion of objects that are launched or thrown. The most common acceleration that affects projectile motion is gravity. If a projectile moves with initial velocity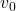
in the gravitational field of the earth, the equation
holds, where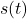
is the traveled distance at time 
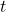. Now let’s explore some real-world examples of this equation:
A Magician in a Wooden Chest
Here is an intriguing example of projectile motion that seeks to determine how much time a magician will have to escape after being fired from a wooden chest using a cannon at a certain height.
A magician is locked in a wooden chest and fired straight up from a powerful cannon. We know that the cannon can launch him up to 50 meters high. However, the critical fact is that the magician has a parachute to land safely, but it won’t work if it’s open less than 25 meters from the ground.
Solution 1
Let’s start by determining the time it takes for the magician to fall back to the ground from a height of 50 meters, the maximum height the cannon can launch him. We will do this by using the standard equation of motion.
When the magician lands safely with his parachute, it means he has traveled 50-25=25 meters since the parachute was opened. We can use this fact and the equation below to solve for the time he takes to reach 25 meters:
Firstly, we know that at a height of 50 meters, the vertical velocity is zero since the magician has just left the cannon. Hence the initial velocity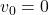
. Secondly, we know that when the magician opens his parachute, he has fallen 25 meters. We can substitute these values into the equation to get:
Solving for t, we get:
Therefore, the magician will have about 1.8 seconds to open his parachute before hitting the ground.
Solution 2
This version of the problem seeks to find out how much time the magician will have to escape from the chest if it takes a dummy six seconds to land on the ground.
Here, we know that the distance the dummy fell is what the magician has to travel to escape the chest. We can solve for the maximum height the magician will reach by using the equation:
The initial velocity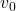
is zero, while we know that it took the dummy six seconds to hit the ground. We can substitute these values into the equation:
Solving for s(6), we get:
Therefore, if the cannon launches the magician to a maximum height of 176.4 meters, he will have six seconds to escape from the wooden chest.
A Football Kicker
Another real-world problem that involves projectile motion is a football kicker. Suppose that a football kicker wants to determine the minimum kick velocity to clear the crossbar of a field goal.
We can use projectile motion equations to solve this problem. Assuming that the kicker launches the ball from the ground (initial height,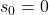
) at an angle 
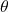with respect to the horizontal and wants the ball to clear a crossbar of 
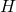meters, we can solve for the minimum kick velocity using the equation:
This equation comes from equating the maximum height of the ball to the height of the crossbar and solving for the minimum initial velocity. Therefore, the solution is independent of the range of the kick.
A Baseball Pitcher
Suppose a baseball pitcher wants to throw the ball with a minimum velocity to reach the catcher at the same height, but with a greater range.
We can use projectile motion equations to solve this problem by assuming that the catcher is at the same height as the pitcher (initial height,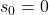
) and is located at a horizontal distance 
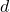away from the pitcher. The pitcher wants to throw the ball with the minimum initial velocity possible so that it will land in the catcher’s hand at the same height but has a longer range.
The minimum initial velocity can be found using the equation:
This equation comes from equating the horizontal distance traveled by the ball to the distance between the pitcher and the catcher, solving for the velocity.
A Rocket Launch
A rocket launch is an excellent example of projectile motion in which the object is blasted upward with an initial velocity. Suppose that we want to determine the maximum height that a rocket can reach.
Using projectile motion equations to solve this problem, we can say that the initial velocity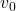
is the velocity at which the rocket is launched. We can solve for the maximum height above the launch site using the equation:
Therefore, the maximum height will depend solely on the initial launch velocity of the rocket.
A Stone Ejected from a Volcano
Another fascinating example of projectile motion is a stone ejected from a volcano. Suppose that we want to determine the maximum height that a stone ejected from a volcano can reach.
We can use projectile motion equations to solve this problem. We assume that the initial velocity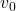
is the velocity at which the stone is ejected upwards from the volcano. We can solve for the maximum height above the volcano using the equation:
Here,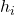
represents the initial height of the volcano before the stone is ejected. Therefore, the maximum height will depend on both the initial launch velocity of the stone and the initial height of the volcano.
Conclusion
Projectile motion plays an essential role in physics as it helps us determine the motion of objects that are thrown or launched in the air. The examples presented here show how real-world problems can be solved by using projectile equations.