If you’re working on a DIY project that involves inserting a metal bar (beam) of square section, , partially into a continuous medium (such as a wall), you may be wondering how the pressure (or force per unit area) is distributed in the contact surfaces between the cantilever beam and the wall when a force is applied to it.
Understanding the scenario
Let’s say the metal bar has a length of that extends into the wall and a length of that extends out of the wall. When a force is applied to the bar, perpendicular to it, we need to know how the pressure is distributed in the surfaces of the beam that are in contact with the wall. The metal bar is considered to have no weight or friction forces, and the system is stable with no displacements. We can assume that the wall is infinite in width, height, and thickness.
The beam inserted into the wall has five surfaces – right, left, top, bottom, and back. If there is no friction, then we can assume that the forces on the right and left surfaces are null. However, we do not know if the forces on the back and top surfaces are also null. The force on the bottom surface must allow the system to remain fixed, but we do not know the distribution of pressure on it.
Solving the problem
One way to simplify the problem is to consider the system to be equivalent to a lever with lengths of and , and the red line in the illustration as the support axis:
/|
/ |
/ |
/ |
/ |
F' / | h
/ |
/ |
/ |
/________|
l
Assuming that the force is applied to the green line in the illustration, the force in the other extreme of the beam becomes . For example, if and , then .
Estimating the forces over the wall
Let’s say you want to stand a TV of 20 kg using a beam – how can you estimate the forces over the wall?
We can use the formula for pressure where is the area of the surface in contact with the wall.
If the cross-sectional area of the beam is , then the area of the surface in contact with the wall is . Thus, the pressure on the surface in contact with the wall is:
Substituting the given values, we get:
Therefore, the pressure on the surface in contact with the wall is directly proportional to the inverse of the area of the beam. This means that if the area of the beam is decreased, the pressure on the surface in contact with the wall will increase.
Conclusion
When inserting a metal bar into a continuous medium such as a wall, it is important to consider how the pressure is distributed in the surfaces of the beam that are in contact with the wall. By simplifying the system to a lever with lengths of and , we can estimate the force on the other extreme of the beam. Using the formula for pressure, we can then calculate the pressure on the surface in contact with the wall. It is important to note that the pressure is directly proportional to the inverse of the area of the beam and that decreasing the area of the beam will increase the pressure on the surface in contact with the wall.
Pressure Done By a Bar/beam Inserted In a Continuous Medium (wall)
If you’re working on a DIY project that involves inserting a metal bar (beam) of square section,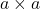 , partially into a continuous medium (such as a wall), you may be wondering how the pressure (or force per unit area) is distributed in the contact surfaces between the cantilever beam and the wall when a force is applied to it.
, partially into a continuous medium (such as a wall), you may be wondering how the pressure (or force per unit area) is distributed in the contact surfaces between the cantilever beam and the wall when a force is applied to it.
Understanding the scenario
Let’s say the metal bar has a length of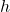 that extends into the wall and a length of
that extends into the wall and a length of 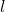 that extends out of the wall. When a force
that extends out of the wall. When a force 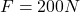 is applied to the bar, perpendicular to it, we need to know how the pressure is distributed in the surfaces of the beam that are in contact with the wall. The metal bar is considered to have no weight or friction forces, and the system is stable with no displacements. We can assume that the wall is infinite in width, height, and thickness.
is applied to the bar, perpendicular to it, we need to know how the pressure is distributed in the surfaces of the beam that are in contact with the wall. The metal bar is considered to have no weight or friction forces, and the system is stable with no displacements. We can assume that the wall is infinite in width, height, and thickness.
The beam inserted into the wall has five surfaces – right, left, top, bottom, and back. If there is no friction, then we can assume that the forces on the right and left surfaces are null. However, we do not know if the forces on the back and top surfaces are also null. The force on the bottom surface must allow the system to remain fixed, but we do not know the distribution of pressure on it.
Solving the problem
One way to simplify the problem is to consider the system to be equivalent to a lever with lengths of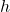 and
and 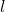 , and the red line in the illustration as the support axis:
, and the red line in the illustration as the support axis:
/| / | / | / | / | F' / | h / | / | / | /________| lAssuming that the force is applied to the green line in the illustration, the force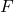 in the other extreme of the beam becomes
in the other extreme of the beam becomes 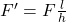 . For example, if
. For example, if 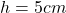 and
and 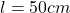 , then
, then 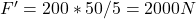 .
.
Estimating the forces over the wall
Let’s say you want to stand a TV of 20 kg using a beam – how can you estimate the forces over the wall?
beam – how can you estimate the forces over the wall?
We can use the formula for pressure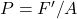 where
where 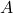 is the area of the surface in contact with the wall.
is the area of the surface in contact with the wall.
If the cross-sectional area of the beam is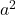 , then the area of the surface in contact with the wall is
, then the area of the surface in contact with the wall is 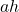 . Thus, the pressure on the surface in contact with the wall is:
. Thus, the pressure on the surface in contact with the wall is:
Substituting the given values, we get:
Therefore, the pressure on the surface in contact with the wall is directly proportional to the inverse of the area of the beam. This means that if the area of the beam is decreased, the pressure on the surface in contact with the wall will increase.
Conclusion
When inserting a metal bar into a continuous medium such as a wall, it is important to consider how the pressure is distributed in the surfaces of the beam that are in contact with the wall. By simplifying the system to a lever with lengths of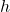 and
and 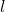 , we can estimate the force on the other extreme of the beam. Using the formula for pressure, we can then calculate the pressure on the surface in contact with the wall. It is important to note that the pressure is directly proportional to the inverse of the area of the beam and that decreasing the area of the beam will increase the pressure on the surface in contact with the wall.
, we can estimate the force on the other extreme of the beam. Using the formula for pressure, we can then calculate the pressure on the surface in contact with the wall. It is important to note that the pressure is directly proportional to the inverse of the area of the beam and that decreasing the area of the beam will increase the pressure on the surface in contact with the wall.