Physics equations are grounded in the basic principle of motion. We use these equations to predict the position of an object in time after knowing its initial position, velocity and acceleration. The motion of particles is determined by external forces acting on them. Therefore, it is essential to understand the nature of these forces to be able to determine the equations of motion accurately. In most cases, equations are second order differential equations. But, what if the equations of motion depend on high time derivatives of the position? In this article, we will discuss this phenomenon and try to explain it through examples.
The Abraham-Lorentz force
The Abraham-Lorentz force is an example of a force that depends on the fourth derivative of the position. This force explains how an electrically charged particle loses energy as it moves. This force can be described as:
This equation shows that the Abraham-Lorentz force is proportional to three time derivatives of the position. Therefore, the resulting equation of motion would be a fourth order differential equation. The solution of this equation depends on the initial conditions of the system. The initial conditions include the position, velocity, acceleration, and the jerk of the particle at a given time.
The Lagrangian equation of motion
The Lagrangian equation of motion is used to describe the motion of particles. It depends only on the coordinates and their first time derivatives. Hence, these are second order differential equations. But, as we saw earlier, there are cases such as the Abraham-Lorentz force where the equation of motion becomes fourth order. One way to deal with such situations is to introduce additional coordinates that depend on high-order derivatives of the position. These coordinates can be treated as “new” coordinates, which, when taken into account, lead to equations of motion that are still second-order differential equations. This technique is called the Ostrogradsky formalism.
The Ostrogradsky formalism introduces new coordinates that depend on the derivatives of the position . Then, the Lagrangian is rewritten to include these coordinates. However, instead of considering as the generalized coordinate, are considered as the generalized coordinates. The Lagrangian of the system can then be written in terms of these generalized coordinates.
Conclusion
In conclusion, there are cases in physics where the equations of motion depend on high-order derivatives of the position. For example, the Abraham-Lorentz force is a fourth-order differential equation that requires knowledge of the initial conditions of the system. In such situations, the Ostrogradsky formalism can be used to introduce new generalized coordinates that depend on high-order derivatives of the position. These new coordinates enable us to rewrite the Lagrangian equation of motion to second-order differential equations. This technique is useful in many areas of physics and is an important tool for solving complex problems.
Is There Any Case In Physics Where the Equations of Motion Depend On High Time Derivatives of the Position?
Physics equations are grounded in the basic principle of motion. We use these equations to predict the position of an object in time after knowing its initial position, velocity and acceleration. The motion of particles is determined by external forces acting on them. Therefore, it is essential to understand the nature of these forces to be able to determine the equations of motion accurately. In most cases, equations are second order differential equations. But, what if the equations of motion depend on high time derivatives of the position? In this article, we will discuss this phenomenon and try to explain it through examples.
The Abraham-Lorentz force
The Abraham-Lorentz force is an example of a force that depends on the fourth derivative of the position. This force explains how an electrically charged particle loses energy as it moves. This force can be described as:
This equation shows that the Abraham-Lorentz force is proportional to three time derivatives of the position. Therefore, the resulting equation of motion would be a fourth order differential equation. The solution of this equation depends on the initial conditions of the system. The initial conditions include the position, velocity, acceleration, and the jerk of the particle at a given time.
The Lagrangian equation of motion
The Lagrangian equation of motion is used to describe the motion of particles. It depends only on the coordinates and their first time derivatives. Hence, these are second order differential equations. But, as we saw earlier, there are cases such as the Abraham-Lorentz force where the equation of motion becomes fourth order. One way to deal with such situations is to introduce additional coordinates that depend on high-order derivatives of the position. These coordinates can be treated as “new” coordinates, which, when taken into account, lead to equations of motion that are still second-order differential equations. This technique is called the Ostrogradsky formalism.
The Ostrogradsky formalism introduces new coordinates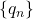
that depend on the derivatives of the position 
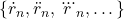. Then, the Lagrangian is rewritten to include these coordinates. However, instead of considering 
as the generalized coordinate,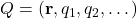 
are considered as the generalized coordinates. The Lagrangian of the system can then be written in terms of these generalized coordinates.
Conclusion
In conclusion, there are cases in physics where the equations of motion depend on high-order derivatives of the position. For example, the Abraham-Lorentz force is a fourth-order differential equation that requires knowledge of the initial conditions of the system. In such situations, the Ostrogradsky formalism can be used to introduce new generalized coordinates that depend on high-order derivatives of the position. These new coordinates enable us to rewrite the Lagrangian equation of motion to second-order differential equations. This technique is useful in many areas of physics and is an important tool for solving complex problems.