Have you ever wondered what formula is used when a ball rolls down an inclined ramp? If you assume the ball is perfectly round and rolls down vertically with no friction, the simplified equation used is . But why is the constant ? Let’s take a closer look.
Potential Energy to Kinetic Energy
If you have an object sliding down a frictionless ramp, the potential energy is converted into kinetic energy after it falls a vertical distance . The formula can be written as:
mgh = 1/2 mv^2
If we manipulate the formula a bit, we can get the acceleration formula of .
Rolling Ball Energy
A ball rolling down an inclined plane has both translational and rotational kinetic energy. This means the potential energy is converted into both translational and rotational kinetic energy. The formula can be written as:
mgh = 1/2 mv^2 + 1/2 I\omega^2
Where is the translational velocity, is the radius of the ball, is the moment of inertia, and is the angular velocity. Using and , we can simplify the formula to:
mgh = 7/10 mv^2
We can then manipulate this formula to get the acceleration of the ball rolling down the inclined plane:
a = 5/7 g \sin\theta
The Constant
Now that we have the correct formula for a ball rolling down an inclined plane, why is the constant used in the simplified formula?
One possible explanation is that it takes into account the rolling friction between the ball and the inclined plane. Rolling friction can be represented by the formula , where is the force of friction, is the coefficient of rolling friction, and is the normal force. We can then use to get:
\mu_f m g \cos\theta = ma
However, we can use the fact that there is no slipping between the ball and the plane to write:
a = r \alpha
where is the radius of the ball and is the angular acceleration. Then, using and , we can write:
F_friction r = I\alpha
Substituting and , we get:
F_friction = 2/5 ma
This means that accounts for of the total force, and the remaining is used for causing acceleration down the inclined plane. Thus, the constant may be used in the simplified formula to account for this relationship between the force of friction and the force used for acceleration down the inclined plane.
Conclusion
The formula for a ball rolling down an inclined plane can be a bit more complicated than initially thought, but it can be derived using principles of energy and friction. While the simplified formula may not be entirely accurate, it can be used as an approximation for certain scenarios.
Formula For a Ball Rolling Down an Inclined Plane
Have you ever wondered what formula is used when a ball rolls down an inclined ramp? If you assume the ball is perfectly round and rolls down vertically with no friction, the simplified equation used is
. But why is the constant 
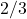? Let’s take a closer look.
Potential Energy to Kinetic Energy
If you have an object sliding down a frictionless ramp, the potential energy is converted into kinetic energy after it falls a vertical distance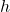
. The formula can be written as:
If we manipulate the formula a bit, we can get the acceleration formula of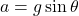
.
Rolling Ball Energy
A ball rolling down an inclined plane has both translational and rotational kinetic energy. This means the potential energy is converted into both translational and rotational kinetic energy. The formula can be written as:
Where
is the translational velocity, 
is the radius of the ball,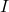 
is the moment of inertia, and 
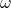is the angular velocity. Using 
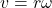and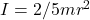 
, we can simplify the formula to:
We can then manipulate this formula to get the acceleration of the ball rolling down the inclined plane:
The Constant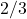
Now that we have the correct formula for a ball rolling down an inclined plane, why is the constant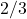
used in the simplified formula?
One possible explanation is that it takes into account the rolling friction between the ball and the inclined plane. Rolling friction can be represented by the formula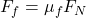
, where 
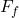is the force of friction, 
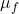is the coefficient of rolling friction, and 
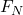is the normal force. We can then use 
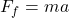to get:
However, we can use the fact that there is no slipping between the ball and the plane to write:
where
is the radius of the ball and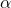 
is the angular acceleration. Then, using 
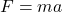and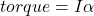 
, we can write:
Substituting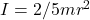
and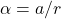 
, we get:
This means that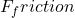
accounts for 
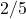of the total force, and the remaining 
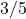is used for causing acceleration down the inclined plane. Thus, the constant 
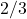may be used in the simplified formula to account for this relationship between the force of friction and the force used for acceleration down the inclined plane.
Conclusion
The formula for a ball rolling down an inclined plane can be a bit more complicated than initially thought, but it can be derived using principles of energy and friction. While the simplified formula
may not be entirely accurate, it can be used as an approximation for certain scenarios.