When working with thermodynamics problems, it is not uncommon to encounter problems where we have to find the temperature of the isotherm for a local minimum of pressure. In this article, we will discuss a problem of this nature and explore a possible solution. We will also touch upon some special cases where the solution becomes non-realistic.
The van der Waals Equation
In this problem, we are dealing with water. Hence, we will use the van der Waals equation:
P = \frac{RT}{V-b}-\frac{a}{V^2}
Here, P is the pressure, V is the volume, T is the temperature, R is the gas constant, a is a parameter related to the intermolecular forces and b is a parameter related to the molecular volume.
Finding the Isotherm
To find the temperature of the isotherm for which the local minimum occurs at , we set:
\frac{\mathrm dP}{\mathrm dV} = 0
Setting this expression to zero and solving for T, we get:
T = \frac{a}{Rb}+\frac{PV}{Rb^2}
Substituting the value of for P, and the values of a and b of water, we get:
T = \frac{0.553}{b}+\frac{100V}{b^2}
Now, we need to solve for V. We first expand the van der Waals equation:
V = -\frac{b+RT}{2}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}
Now, we substitute this expression for V in the expression for T :
T = \frac{0.553}{b}+\frac{100}{b^2}\left(-\frac{b+RT}{2}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}\right)
This equation is somewhat intractable and we have to resort to numerical methods to solve for T.
Realistic Solutions
When we solve the equation for T, we get a solution which is of the order of . This is not a realistic value and suggests that the problem setter might have made an error. Perhaps, the intended value was instead of ?
Alternatively, we could look at the equation for V. It is possible that for some values of P, the expression under the cube roots could be negative. In such cases, Cardano’s formula does not have a real solution for V.
Conclusion
In this article, we discussed a problem of finding the temperature of the isotherm for a local minimum of pressure. We explored a possible solution using the van der Waals equation and Cardano’s formula. We also touched upon some special cases where the solution becomes non-realistic.
Finding the Isotherm With Given Minima
When working with thermodynamics problems, it is not uncommon to encounter problems where we have to find the temperature of the isotherm for a local minimum of pressure. In this article, we will discuss a problem of this nature and explore a possible solution. We will also touch upon some special cases where the solution becomes non-realistic.
The van der Waals Equation
In this problem, we are dealing with water. Hence, we will use the van der Waals equation:
P = \frac{RT}{V-b}-\frac{a}{V^2}Here,
Pis the pressure,Vis the volume,Tis the temperature,Ris the gas constant,ais a parameter related to the intermolecular forces andbis a parameter related to the molecular volume.Finding the Isotherm
To find the temperature of the isotherm for which the local minimum occurs at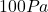
, we set:
\frac{\mathrm dP}{\mathrm dV} = 0Setting this expression to zero and solving for
T, we get:T = \frac{a}{Rb}+\frac{PV}{Rb^2}Substituting the value of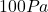
for
P, and the values ofaandbof water, we get:T = \frac{0.553}{b}+\frac{100V}{b^2}Now, we need to solve for
V. We first expand the van der Waals equation:We can solve for
Vusing Cardano’s formula:where:
\alpha = \sqrt[3]{\frac{(b+RT)^2}{4}-\frac{a}{2}-\frac{b^3P}{27}}\beta = -\frac{b+RT}{2}\gamma = \sqrt[3]{\frac{(b+RT)^2}{4}-\frac{a}{2}-\frac{b^3P}{27}}Substituting the values of
P,T,aandb, we get:V = -\frac{b+RT}{2}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}Now, we substitute this expression for
Vin the expression forT:T = \frac{0.553}{b}+\frac{100}{b^2}\left(-\frac{b+RT}{2}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}\right)This expression simplifies to:
200 = RT+\frac{553}{b}-\frac{200}{b}-\frac{a}{b^2}\left(\frac{2}{b+RT}+\frac{1}{b+RT+\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}}+\frac{1}{b+RT-\sqrt[3]{\frac{(b+RT)^3}{8}+\frac{RbT}{2}-\frac{a}{4}}}\right)This equation is somewhat intractable and we have to resort to numerical methods to solve for
T.Realistic Solutions
When we solve the equation for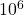
. This is not a realistic value and suggests that the problem setter might have made an error. Perhaps, the intended value was 
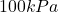instead of 
?
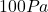T, we get a solution which is of the order ofAlternatively, we could look at the equation for
V. It is possible that for some values ofP, the expression under the cube roots could be negative. In such cases, Cardano’s formula does not have a real solution forV.Conclusion
In this article, we discussed a problem of finding the temperature of the isotherm for a local minimum of pressure. We explored a possible solution using the van der Waals equation and Cardano’s formula. We also touched upon some special cases where the solution becomes non-realistic.