Understanding Cauchy-Schwarz Integral Screening and Different Inequalities
In the field of molecular electronic structure theory, Cauchy-Schwarz integral screening is an important concept that is used to estimate the two-electron integrals in atomic orbital (AO) basis. In this article, we will explore different inequalities that can be derived from Cauchy-Schwarz integral screening, specifically Ineq. 1-6, as described in Eq. (9.12.23) in [1].
What is Cauchy-Schwarz Integral Screening?
Cauchy-Schwarz integral screening is a mathematical technique used to estimate the two-electron integrals in AO basis. In general, two-electron integrals are computationally expensive and can significantly increase the computational cost of electronic structure calculations. Cauchy-Schwarz integral screening reduces the number of two-electron integrals that need to be computed by using a set of screening criteria to identify integrals that are sufficiently small and can be safely neglected.
Deriving Ineq. 1-6
Eq. (9.12.23) in [1] states that:
(MEST 9.12.23)
Here, the terms refer to distribution coefficients and the terms refer to two-electron integrals. By setting and , we get:
This is a straightforward inequality that holds when is a real number. It follows that:
(MEST 9.12.24)
This inequality satisfies the requirements of the Cauchy-Schwarz inequality, which leads to:
(MEST 9.12.25)
Now, since , we can derive the following inequality:
(1)
which in turn leads to:
(2)
This inequality also meets the requirements of the Cauchy-Schwarz inequality, which results in:
(3)
By manipulating the indices further, we get a set of six different inequalities:
(Ineq. 1)
(Ineq. 2)
(Ineq. 3)
(Ineq. 4)
(Ineq. 5)
(Ineq. 6)
Practical Applications
In practice, all of these inequalities are used, depending on the specifics of the electronic structure calculation being performed. However, Ineq. 1 is the most commonly cited inequality, as it is the most straightforward to derive and understand. Ineq. 2-6 are essentially extensions of Ineq. 1, and are used when specific arrangements of the indices are present in the electronic structure calculation.
By using Cauchy-Schwarz integral screening and the resulting inequalities, it is possible to drastically reduce the computational cost of two-electron integral calculations. This is extremely important in modern electronic structure calculations, which deal with systems that can contain thousands of electrons and tens of thousands of basis functions.
Conclusion
Cauchy-Schwarz integral screening is a powerful mathematical technique that allows for the efficient estimation of two-electron integrals in electronic structure calculations. By understanding the different inequalities that can be derived from this technique, researchers can tailor their calculations to reduce computational costs and improve accuracy. By using Cauchy-Schwarz integral screening and the resulting inequalities, it is possible to perform electronic structure calculations on larger and more complex systems, which has important applications in fields like material science, drug discovery, and more.
Cauchy-schwarz Integral Screening Different Inequalites
Understanding Cauchy-Schwarz Integral Screening and Different Inequalities
In the field of molecular electronic structure theory, Cauchy-Schwarz integral screening is an important concept that is used to estimate the two-electron integrals in atomic orbital (AO) basis. In this article, we will explore different inequalities that can be derived from Cauchy-Schwarz integral screening, specifically Ineq. 1-6, as described in Eq. (9.12.23) in [1].
What is Cauchy-Schwarz Integral Screening?
Cauchy-Schwarz integral screening is a mathematical technique used to estimate the two-electron integrals in AO basis. In general, two-electron integrals are computationally expensive and can significantly increase the computational cost of electronic structure calculations. Cauchy-Schwarz integral screening reduces the number of two-electron integrals that need to be computed by using a set of screening criteria to identify integrals that are sufficiently small and can be safely neglected.
Deriving Ineq. 1-6
Eq. (9.12.23) in [1] states that:
Here, the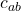
terms refer to distribution coefficients and the 
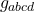terms refer to two-electron integrals. By setting 
and 
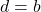, we get:
This is a straightforward inequality that holds when
is a real number. It follows that:
This inequality satisfies the requirements of the Cauchy-Schwarz inequality, which leads to:
Now, since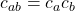
, we can derive the following inequality:
which in turn leads to:
This inequality also meets the requirements of the Cauchy-Schwarz inequality, which results in:
By manipulating the indices further, we get a set of six different inequalities:
Practical Applications
In practice, all of these inequalities are used, depending on the specifics of the electronic structure calculation being performed. However, Ineq. 1 is the most commonly cited inequality, as it is the most straightforward to derive and understand. Ineq. 2-6 are essentially extensions of Ineq. 1, and are used when specific arrangements of the indices are present in the electronic structure calculation.
By using Cauchy-Schwarz integral screening and the resulting inequalities, it is possible to drastically reduce the computational cost of two-electron integral calculations. This is extremely important in modern electronic structure calculations, which deal with systems that can contain thousands of electrons and tens of thousands of basis functions.
Conclusion
Cauchy-Schwarz integral screening is a powerful mathematical technique that allows for the efficient estimation of two-electron integrals in electronic structure calculations. By understanding the different inequalities that can be derived from this technique, researchers can tailor their calculations to reduce computational costs and improve accuracy. By using Cauchy-Schwarz integral screening and the resulting inequalities, it is possible to perform electronic structure calculations on larger and more complex systems, which has important applications in fields like material science, drug discovery, and more.