How to Calculate the Relationship Between the Pressures of Zinc, Carbon Monoxide, and Carbon Dioxide
Chemical reactions can be tricky to understand, but with a little bit of guidance, they can be easier to comprehend. In this article, we will be focusing on how to calculate the relationship between the pressures of zinc, carbon monoxide, and carbon dioxide based on mole balance.
Problem Statement
Let’s start with the problem statement. We have zinc oxide, which is being reduced at a constant temperature in a closed reactor using and as the only starting materials. The following reactions are assumed to be at thermodynamic equilibrium.
*** QuickLaTeX cannot compile formula:
\begin{align*}
\ce{ZnO(s) + C(s) &-> Zn(g) + CO(g)}\\
\ce{2CO(g) &-> CO2(g) + C(s)}
\end{align*}
*** Error message:
Undefined control sequence \ce.
leading text: \end{align*}
Missing } inserted.
leading text: \end{align*}
Missing { inserted.
leading text: \end{align*}
Missing } inserted.
leading text: \end{align*}
Missing { inserted.
leading text: \end{align*}
Missing } inserted.
leading text: \end{align*}
Missing \endgroup inserted.
leading text: \end{align*}
Argument of \@tempb has an extra }.
leading text: \end{align*}
Paragraph ended before \@tempb was complete.
leading text: \end{align*}
Missing $ inserted.
leading text: \end{align*}
Incomplete \if; all text was ignored after line 11.
Forbidden control sequence found while scanning definition of \@tempa.
leading text: \end{align*}
Missing $ inserted.
leading text: \end{align*}
Missing \endgroup inserted.
Our goal is to determine the relationship, based on mole balance, that is applicable to the system at equilibrium. We have been provided with four options, such as:
(A)
It’s worth noting here that we must assume ideal gas behavior for these calculations.
Solution Approach
Now that we know the problem statement let’s try to find the solution step by step.
Step 1: Balance the equations.
The first thing we need to do is balance the given equations. The balanced equations are as follows:
*** QuickLaTeX cannot compile formula:
\begin{align*}
\ce{ZnO(s) + C(s) &-> Zn(g) + CO(g)}\\
\ce{2CO(g) &-> CO2(g) + 2C(s)}
\end{align*}
*** Error message:
Undefined control sequence \ce.
leading text: \end{align*}
Missing } inserted.
leading text: \end{align*}
Missing { inserted.
leading text: \end{align*}
Missing } inserted.
leading text: \end{align*}
Missing { inserted.
leading text: \end{align*}
Missing } inserted.
leading text: \end{align*}
Missing \endgroup inserted.
leading text: \end{align*}
Argument of \@tempb has an extra }.
leading text: \end{align*}
Paragraph ended before \@tempb was complete.
leading text: \end{align*}
Missing $ inserted.
leading text: \end{align*}
Incomplete \if; all text was ignored after line 11.
Forbidden control sequence found while scanning definition of \@tempa.
leading text: \end{align*}
Missing $ inserted.
leading text: \end{align*}
Missing \endgroup inserted.
As the equations are now balanced, we can move on to the next step.
Step 2: Find the mole balance.
The mole balance is crucial to solving this problem. It is defined as:
mole of component entering the system = mole of component leaving the system
Based on this, let’s create a chart for each component.
Now that we have established the mole balance let’s move on to the next step.
Step 3: Relate pressures based on mole balance.
Now that we have the mole balances for each component, we can relate the pressures using the ideal gas law. The ideal gas law is:
PV = nRT
P = nRT/V
where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the temperature.
Let’s relate the pressures by using the mole balances we found earlier.
Pressure Relationship
We can solve the equation by using any of the mole balance relationships provided in the options. Let’s try to solve for each option one by one.
Option A:
(3)
Plugging the mole balances for each component, we get:
(4)
We can see that option A is valid based on the mole balance equation. Let’s try another option.
Option B:
(5)
We can see that this option is not valid based on the mole balance equation as it doesn’t match the equation calculated for Zn in Step 2.
Option C:
(6)
This option is also valid based on the mole balance equation. Let’s try the last option.
Option D:
(7)
This option is also valid based on the mole balance equation.
Conclusion
Based on the mole balance equations we calculated, we can see that three out of four options are valid for calculating the relationship between the pressures of zinc, carbon monoxide, and carbon dioxide. The correct options are A, C, and D, and the incorrect option is B. By following these steps, we can easily calculate the relationship between the pressures of different components based on mole balance.
Chemistry can be challenging, but by breaking down problems into smaller parts, it can be easier to understand. These types of problems are common in the field of chemistry and are essential in determining the behavior of different chemical reactions under different conditions.
How to Calculate the Relationship Between the Pressures of Zinc, Carbon Monoxide, And Carbon Dioxide Based On Mole Balance?
How to Calculate the Relationship Between the Pressures of Zinc, Carbon Monoxide, and Carbon Dioxide
Chemical reactions can be tricky to understand, but with a little bit of guidance, they can be easier to comprehend. In this article, we will be focusing on how to calculate the relationship between the pressures of zinc, carbon monoxide, and carbon dioxide based on mole balance.
Problem Statement
Let’s start with the problem statement. We have zinc oxide, which is being reduced at a constant temperature in a closed reactor using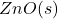 and
and 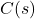 as the only starting materials. The following reactions are assumed to be at thermodynamic equilibrium.
as the only starting materials. The following reactions are assumed to be at thermodynamic equilibrium.