Albert Einstein’s famous equation is well-known for its contributions to nuclear physics. However, this equation has a much wider scope than what it is usually credited for. In this article, we explore the various applications of this mass-energy equivalence equation outside the realm of nuclear physics.
What is ?
Before we delve into the scope of the equation, let us first understand what it means. The equation states that the energy () of an object is equal to its mass () multiplied by the speed of light squared (). This equation shows that mass and energy are interchangeable and can be converted into one another.
The Scope of
While is predominantly attributed to nuclear physics, its scope extends far beyond it. Here are some examples of its applications in different fields:
Particle Physics
In particle physics, is used in experiments that involve the creation of particles. When high energy particles collide, they create new particles with higher masses. This increased mass is due to the energy that has been converted from kinetic to mass energy. This principle is used in experiments to study particle interactions.
Astronomy
According to the theory of relativity, energy and mass are related. In astronomy, this relationship is used to understand black holes. As objects get closer to the event horizon of a black hole, they gain speed and their energy increases. The increased energy leads to an increase in mass, which makes the object harder to escape the gravitational pull of the black hole.
Meteorology
is also used in meteorology to calculate the amount of energy required to create thunderstorms. Thunderstorms are created when air rises and cools in the atmosphere, resulting in the release of energy in the form of lightning. The amount of energy released is calculated using .
Measuring
To measure the amount of energy stored in an object’s mass, we can use the equation . One practical application of this equation is in nuclear power plants. In a nuclear power plant, uranium atoms are split, releasing energy in the form of radiation. The radiation heats water, which creates steam to turn a turbine, generating electricity.
The amount of energy released in a nuclear reaction can be calculated using . For example, if one gram of uranium is completely converted to energy, it would release approximately 9*10^13 joules of energy—equivalent to the energy produced by burning 21,000 tons of coal.
Conclusion
We hope this article has provided a clear understanding of the scope of . While its most popular application is in nuclear physics, it is fascinating to see the widespread impact that this equation has had on different fields. From meteorology to particle physics, this equation has allowed us to understand the relationship between mass and energy and its applications in various disciplines.
Scope of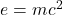
Exploring the Scope of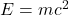
Albert Einstein’s famous equation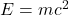
is well-known for its contributions to nuclear physics. However, this equation has a much wider scope than what it is usually credited for. In this article, we explore the various applications of this mass-energy equivalence equation outside the realm of nuclear physics.
What is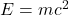
?
Before we delve into the scope of the equation, let us first understand what it means. The equation states that the energy (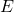
) of an object is equal to its mass (
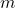) multiplied by the speed of light squared (
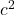). This equation shows that mass and energy are interchangeable and can be converted into one another.
The Scope of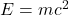
While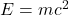
is predominantly attributed to nuclear physics, its scope extends far beyond it. Here are some examples of its applications in different fields:
Particle Physics
In particle physics,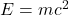
is used in experiments that involve the creation of particles. When high energy particles collide, they create new particles with higher masses. This increased mass is due to the energy that has been converted from kinetic to mass energy. This principle is used in experiments to study particle interactions.
Astronomy
According to the theory of relativity, energy and mass are related. In astronomy, this relationship is used to understand black holes. As objects get closer to the event horizon of a black hole, they gain speed and their energy increases. The increased energy leads to an increase in mass, which makes the object harder to escape the gravitational pull of the black hole.
Meteorology
Measuring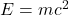
To measure the amount of energy stored in an object’s mass, we can use the equation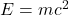
. One practical application of this equation is in nuclear power plants. In a nuclear power plant, uranium atoms are split, releasing energy in the form of radiation. The radiation heats water, which creates steam to turn a turbine, generating electricity.
The amount of energy released in a nuclear reaction can be calculated using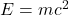
. For example, if one gram of uranium is completely converted to energy, it would release approximately 9*10^13 joules of energy—equivalent to the energy produced by burning 21,000 tons of coal.
Conclusion
We hope this article has provided a clear understanding of the scope of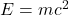
. While its most popular application is in nuclear physics, it is fascinating to see the widespread impact that this equation has had on different fields. From meteorology to particle physics, this equation has allowed us to understand the relationship between mass and energy and its applications in various disciplines.