Metronomes are common tools for musicians to maintain a consistent tempo while playing an instrument. These tools work on the principle of a weighted pendulum, where a weight moves back and forth, producing a clicking sound with each oscillation. A metronome typically allows a wide range of tempos, between 40-208 beats per minute (bpm) in a short distance. In this article, we will explore the working principle of a metronome and how it allows such a wide range of tempos.
Working Principle of a Metronome
A metronome is essentially a double-weighted pendulum, consisting of a rod with a movable weight at one end and a fixed counterweight at the other end. The weight at the movable end moves back and forth as the rod oscillates, producing the clicking sound. The weight at the fixed end acts as a stabilizing force, ensuring that the pendulum maintains a consistent oscillation.
Deriving an Equation for the Natural Frequency of the System
To understand how a metronome allows such a wide range of tempos, we can derive an equation for the natural frequency of the system. Let be the mass of the movable weight, the distance of ‘s center of mass from the rotation point, the mass of the fixed counterweight, and the distance of ‘s center of mass from the rotation point.
Angular Equation of Motion
We can set up the angular equation of motion as:
Where is the angle of oscillation, is the acceleration due to gravity, and is the second derivative of with respect to time.
Small Angle Approximation
As the oscillations are small, we can approximate and obtain:
Natural Angular Frequency
From the above equation, we can derive the natural angular frequency:
Converting to Beats Per Minute
We can convert the natural angular frequency to beats per minute by noting that a metronome beats twice per cycle, resulting in:
Understanding the Range of Tempos for a Metronome
The range of tempos for a metronome is typically between 40-208 bpm, with 208 bpm being the closest marked tempo to the rotation point, and 40 bpm the farthest. As the counterweight is fixed, the bpm equation is essentially a function of .
If we fix particular values of , , and , then we can find how long of a rod we need (i.e. the range of values for for tempos between 40 and 208 bpm). For instance, if we set bpm=208 (and grams, grams, and around 20 mm), we can solve for , and we get reasonable answers on the order of a few centimeters.
Potential Sources of Error
However, when we try to solve for the value of for bpm=40, we get values on the order of meters, which is much longer than an actual metronome rod. This leads us to question if our analysis is correct and what is causing such a dramatic error in the length of the rod.
Some assumptions that we have made in the analysis could result in these errors:
We have assumed that the rod has negligible mass, although this seems reasonable looking at a typical metronome.
We have approximated the two masses as point masses, since the moment of inertia of the system is the denominator of the term.
We have neglected frictional losses/the type of frictional loss present. Including a loss term proportional to the speed could make a difference, but we’ve seen that metronomes are typically modeled with a Van der Pol loss term.
We have neglected the effect of the escapement, the gear-spring mechanism that regulates the amplitude of the metronome.
Further analysis is required to understand the full extent of the errors and how they could be minimized.
How Does a Metronome Allow Such a Wide Range of Tempos In Such a Short Distance?
Metronomes are common tools for musicians to maintain a consistent tempo while playing an instrument. These tools work on the principle of a weighted pendulum, where a weight moves back and forth, producing a clicking sound with each oscillation. A metronome typically allows a wide range of tempos, between 40-208 beats per minute (bpm) in a short distance. In this article, we will explore the working principle of a metronome and how it allows such a wide range of tempos.
Working Principle of a Metronome
A metronome is essentially a double-weighted pendulum, consisting of a rod with a movable weight at one end and a fixed counterweight at the other end. The weight at the movable end moves back and forth as the rod oscillates, producing the clicking sound. The weight at the fixed end acts as a stabilizing force, ensuring that the pendulum maintains a consistent oscillation.
Deriving an Equation for the Natural Frequency of the System
To understand how a metronome allows such a wide range of tempos, we can derive an equation for the natural frequency of the system. Let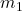 be the mass of the movable weight,
be the mass of the movable weight, 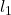 the distance of
the distance of 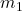 ‘s center of mass from the rotation point,
‘s center of mass from the rotation point, 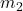 the mass of the fixed counterweight, and
the mass of the fixed counterweight, and 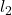 the distance of
the distance of 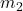 ‘s center of mass from the rotation point.
‘s center of mass from the rotation point.
Angular Equation of Motion
We can set up the angular equation of motion as:
Where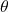 is the angle of oscillation,
is the angle of oscillation, 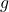 is the acceleration due to gravity, and
is the acceleration due to gravity, and 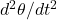 is the second derivative of
is the second derivative of 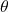 with respect to time.
with respect to time.
Small Angle Approximation
As the oscillations are small, we can approximate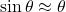 and obtain:
and obtain:
Natural Angular Frequency
From the above equation, we can derive the natural angular frequency:
Converting to Beats Per Minute
We can convert the natural angular frequency to beats per minute by noting that a metronome beats twice per cycle, resulting in:
Understanding the Range of Tempos for a Metronome
The range of tempos for a metronome is typically between 40-208 bpm, with 208 bpm being the closest marked tempo to the rotation point, and 40 bpm the farthest. As the counterweight is fixed, the bpm equation is essentially a function of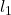 .
.
If we fix particular values of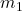 ,
, 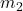 , and
, and 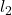 , then we can find how long of a rod we need (i.e. the range of values for
, then we can find how long of a rod we need (i.e. the range of values for 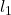 for tempos between 40 and 208 bpm). For instance, if we set bpm=208 (and
for tempos between 40 and 208 bpm). For instance, if we set bpm=208 (and 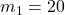 grams,
grams, 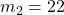 grams, and
grams, and 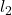 around 20 mm), we can solve for
around 20 mm), we can solve for 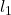 , and we get reasonable answers on the order of a few centimeters.
, and we get reasonable answers on the order of a few centimeters.
Potential Sources of Error
However, when we try to solve for the value of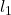 for bpm=40, we get values on the order of meters, which is much longer than an actual metronome rod. This leads us to question if our analysis is correct and what is causing such a dramatic error in the length of the rod.
for bpm=40, we get values on the order of meters, which is much longer than an actual metronome rod. This leads us to question if our analysis is correct and what is causing such a dramatic error in the length of the rod.
Some assumptions that we have made in the analysis could result in these errors:
Further analysis is required to understand the full extent of the errors and how they could be minimized.