There are various assumptions that one can make to simplify the equation of radiation transfer given in (1.1). In this article, we explore some plausible and creative assumptions for modelling radiative transfer of heat from the atmosphere to terrestrial solar cells.
Introduction
The equation of radiation transfer given in (1.1) describes the transfer of radiant energy through a medium, and is a fundamental equation in atmospheric radiation. It governs the propagation of radiation through a medium, and is often used in climate modelling, remote sensing and astrophysics.
In the context of modelling radiative transfer of heat from the atmosphere to terrestrial solar cells, we can make some assumptions to simplify the equation. For instance, we may assume that the scattering opacity , which simplifies the equation considerably.
The Reduced Form of (1.1)
The first term in (1.1) represents the time derivative of the intensity of radiation , while the second term represents the spatial derivative of in the direction of the unit vector . The third term is a sum of the absorption and scattering opacities. The fourth term represents the emission of radiation by the medium, while the fifth term represents the scattering of radiation by the medium in all directions.
Assuming , we get the reduced form of (1.1) as:
In this reduced form, we still have the time derivative term and the spatial derivative term, but the term involving the scattering opacity has disappeared. This is a reasonable assumption to make in many practical situations, where the scattering of radiation can be small compared to its absorption.
The second term in the reduced form of (1.1) can be expressed as a scalar value by taking the dot product of with . This greatly simplifies the equation and makes it more amenable for analytical or numerical solutions.
Further Reduction on Physical Grounds
Can the reduced form of (1.1) be further simplified on physical grounds? This is a question that depends on the specific details of the problem at hand. However, there are some general considerations that may help in simplifying the equation further.
For example, in the case of heat radiation from the atmosphere to a flat surface like a solar cell, we can assume that the radiation is incident from a single direction, namely downwards in the direction of gravity. This means we can treat the radiation as being independent of the azimuthal angle (the angle in the plane perpendicular to the direction of gravity).
This assumption greatly simplifies the integration in the last term of (1.1), which involves integrating over all directions in space. We can then write:
where is the polar angle (the angle between the radiation direction and the normal to the surface), and is the critical angle beyond which radiation is fully reflected by the surface. This effectively reduces the dimensionality of the problem and makes it more tractable.
Conclusion
In conclusion, the equation of radiation transfer given in (1.1) can be simplified by making reasonable assumptions depending on the specific details of the problem. For example, assuming zero scattering opacity and a single incident direction of radiation can greatly simplify the equation and make it more amenable for analytical and numerical solutions.
It is worth noting that these assumptions are not always applicable, and in some cases, they may lead to erroneous results. Therefore, it is important to carefully consider the assumptions made when using simplified models, and to validate the results against more complex models before making any conclusions.
Code Example:
# Python code for solving the reduced form of (1.1)
import numpy as np
# Define the parameters of the problem
k_a = 1.0
j = 0.0
k_s = 0.0
# Define the mesh and discretize the space and time
dt = 0.01
dx = 0.1
tmax = 1.0
xmax = 1.0
nsteps = int(tmax/dt)
npoints = int(xmax/dx)
# Set the initial condition
I = np.zeros((npoints, nsteps))
I[:, 0] = 1.0
# Time-stepping loop
for i in range(nsteps-1):
for j in range(1, npoints-1):
I[j, i+1] = I[j, i] + (k_a*I[j, i] + j)*dt/dx**2 + I[j+1, i]*dt/dx**2 - 2*I[j, i]*dt/dx**2 + I[j-1, i]*dt/dx**2
# Plot the results
import matplotlib.pyplot as plt
plt.imshow(I, aspect='auto', extent=[0, tmax, 0, xmax])
plt.colorbar()
plt.xlabel('Time')
plt.ylabel('Space')
plt.show()
Plausible/ Creative Assumptions For Solving Equation of Radiation Transfer
There are various assumptions that one can make to simplify the equation of radiation transfer given in (1.1). In this article, we explore some plausible and creative assumptions for modelling radiative transfer of heat from the atmosphere to terrestrial solar cells.
Introduction
The equation of radiation transfer given in (1.1) describes the transfer of radiant energy through a medium, and is a fundamental equation in atmospheric radiation. It governs the propagation of radiation through a medium, and is often used in climate modelling, remote sensing and astrophysics.
In the context of modelling radiative transfer of heat from the atmosphere to terrestrial solar cells, we can make some assumptions to simplify the equation. For instance, we may assume that the scattering opacity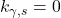 , which simplifies the equation considerably.
, which simplifies the equation considerably.
The Reduced Form of (1.1)
The first term in (1.1) represents the time derivative of the intensity of radiation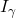 , while the second term represents the spatial derivative of
, while the second term represents the spatial derivative of 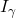 in the direction of the unit vector
in the direction of the unit vector 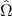 . The third term is a sum of the absorption and scattering opacities. The fourth term represents the emission of radiation by the medium, while the fifth term represents the scattering of radiation by the medium in all directions.
. The third term is a sum of the absorption and scattering opacities. The fourth term represents the emission of radiation by the medium, while the fifth term represents the scattering of radiation by the medium in all directions.
Assuming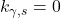 , we get the reduced form of (1.1) as:
, we get the reduced form of (1.1) as:
In this reduced form, we still have the time derivative term and the spatial derivative term, but the term involving the scattering opacity has disappeared. This is a reasonable assumption to make in many practical situations, where the scattering of radiation can be small compared to its absorption.
The second term in the reduced form of (1.1) can be expressed as a scalar value by taking the dot product of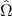 with
with 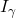 . This greatly simplifies the equation and makes it more amenable for analytical or numerical solutions.
. This greatly simplifies the equation and makes it more amenable for analytical or numerical solutions.
Further Reduction on Physical Grounds
Can the reduced form of (1.1) be further simplified on physical grounds? This is a question that depends on the specific details of the problem at hand. However, there are some general considerations that may help in simplifying the equation further.
For example, in the case of heat radiation from the atmosphere to a flat surface like a solar cell, we can assume that the radiation is incident from a single direction, namely downwards in the direction of gravity. This means we can treat the radiation as being independent of the azimuthal angle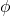 (the angle in the plane perpendicular to the direction of gravity).
(the angle in the plane perpendicular to the direction of gravity).
This assumption greatly simplifies the integration in the last term of (1.1), which involves integrating over all directions in space. We can then write:
where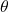 is the polar angle (the angle between the radiation direction and the normal to the surface), and
is the polar angle (the angle between the radiation direction and the normal to the surface), and 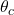 is the critical angle beyond which radiation is fully reflected by the surface. This effectively reduces the dimensionality of the problem and makes it more tractable.
is the critical angle beyond which radiation is fully reflected by the surface. This effectively reduces the dimensionality of the problem and makes it more tractable.
Conclusion
In conclusion, the equation of radiation transfer given in (1.1) can be simplified by making reasonable assumptions depending on the specific details of the problem. For example, assuming zero scattering opacity and a single incident direction of radiation can greatly simplify the equation and make it more amenable for analytical and numerical solutions.
It is worth noting that these assumptions are not always applicable, and in some cases, they may lead to erroneous results. Therefore, it is important to carefully consider the assumptions made when using simplified models, and to validate the results against more complex models before making any conclusions.
Code Example: # Python code for solving the reduced form of (1.1) import numpy as np # Define the parameters of the problem k_a = 1.0 j = 0.0 k_s = 0.0 # Define the mesh and discretize the space and time dt = 0.01 dx = 0.1 tmax = 1.0 xmax = 1.0 nsteps = int(tmax/dt) npoints = int(xmax/dx) # Set the initial condition I = np.zeros((npoints, nsteps)) I[:, 0] = 1.0 # Time-stepping loop for i in range(nsteps-1): for j in range(1, npoints-1): I[j, i+1] = I[j, i] + (k_a*I[j, i] + j)*dt/dx**2 + I[j+1, i]*dt/dx**2 - 2*I[j, i]*dt/dx**2 + I[j-1, i]*dt/dx**2 # Plot the results import matplotlib.pyplot as plt plt.imshow(I, aspect='auto', extent=[0, tmax, 0, xmax]) plt.colorbar() plt.xlabel('Time') plt.ylabel('Space') plt.show()