Insulation is a critical component in many industries, from electrical wiring to steam pipes. But there is a critical thickness of the insulation below which it can actually increase heat transfer instead of decreasing it. This effect is due to the thermal resistance of the insulation material being lower than the decrease in resistance to convection caused by the increased surface area due to the thicker insulation. In this article, we will explore the values of critical thickness of insulation in various realistic cases.
Understanding the Equation
The equation for the critical thickness of insulation is given by:
Here, is the critical radius, is the thermal conductivity of the insulation material, and is the convective heat transfer coefficient.
To find the critical thickness of insulation for different materials and applications, we need to determine the values of and .
Evaluating Critical Thickness for Realistic Cases
For an electrical wire, the critical thickness of insulation can be calculated using the values of and for air at standard temperature and pressure (STP). The thermal conductivity of common insulation materials such as PVC, rubber, and nylon are in the range of 0.1-0.2 W/mK, while the heat transfer coefficient of air is about 5 W/m2K.
Substituting these values in the equation, we get:
This gives a range of 0.02-0.04 meter for the critical radius, which translates to 2-4 centimeters for the critical thickness of insulation.
Similarly, for a steam pipe or a water pipe, we need to take into account the temperature difference between the fluid flowing inside and the surrounding environment. The thermal conductivity of insulation materials decreases with increasing temperature, while the convective heat transfer coefficient increases. This means that the critical thickness of insulation will be lower for higher temperature applications.
Practical Importance of Critical Thickness
Fundamentals of Heat and Mass Transfer 6e by Incropera et al. indicates that the effect of critical thickness of insulation is usually too small to be of practical importance. In most cases, the values of and are such that the critical thickness of insulation is much less than the thickness required for effective thermal insulation.
However, in certain applications such as cryogenic piping or high temperature processing, the critical thickness of insulation can have practical implications. In these cases, it is important to carefully select the type and thickness of insulation material to optimize the thermal resistance.
Conclusion
In conclusion, the critical thickness of insulation is an important concept in heat transfer engineering. It is the minimum thickness of insulation below which it can increase heat transfer instead of reducing it. The value of critical thickness depends on the type of insulation material, the convective heat transfer coefficient, and the temperature difference between the fluid and the surrounding environment. While the effect is usually too small to be of practical importance, in certain applications it can have significant implications for thermal resistance.
What are Typical Values of the Critical Thickness of Insulation? [closed]
What is the Critical Thickness of Insulation?
Insulation is a critical component in many industries, from electrical wiring to steam pipes. But there is a critical thickness of the insulation below which it can actually increase heat transfer instead of decreasing it. This effect is due to the thermal resistance of the insulation material being lower than the decrease in resistance to convection caused by the increased surface area due to the thicker insulation. In this article, we will explore the values of critical thickness of insulation in various realistic cases.
Understanding the Equation
The equation for the critical thickness of insulation is given by:
Here,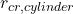
is the critical radius, 
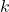is the thermal conductivity of the insulation material, and 
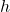is the convective heat transfer coefficient.
To find the critical thickness of insulation for different materials and applications, we need to determine the values of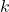
and 
.
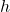Evaluating Critical Thickness for Realistic Cases
For an electrical wire, the critical thickness of insulation can be calculated using the values of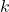
and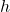 
for air at standard temperature and pressure (STP). The thermal conductivity of common insulation materials such as PVC, rubber, and nylon are in the range of 0.1-0.2 W/mK, while the heat transfer coefficient of air is about 5 W/m2K.
Substituting these values in the equation, we get:
This gives a range of 0.02-0.04 meter for the critical radius, which translates to 2-4 centimeters for the critical thickness of insulation.
Similarly, for a steam pipe or a water pipe, we need to take into account the temperature difference between the fluid flowing inside and the surrounding environment. The thermal conductivity of insulation materials decreases with increasing temperature, while the convective heat transfer coefficient increases. This means that the critical thickness of insulation will be lower for higher temperature applications.
Practical Importance of Critical Thickness
Fundamentals of Heat and Mass Transfer 6e by Incropera et al. indicates that the effect of critical thickness of insulation is usually too small to be of practical importance. In most cases, the values of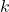
and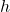 
are such that the critical thickness of insulation is much less than the thickness required for effective thermal insulation.
However, in certain applications such as cryogenic piping or high temperature processing, the critical thickness of insulation can have practical implications. In these cases, it is important to carefully select the type and thickness of insulation material to optimize the thermal resistance.
Conclusion
In conclusion, the critical thickness of insulation is an important concept in heat transfer engineering. It is the minimum thickness of insulation below which it can increase heat transfer instead of reducing it. The value of critical thickness depends on the type of insulation material, the convective heat transfer coefficient, and the temperature difference between the fluid and the surrounding environment. While the effect is usually too small to be of practical importance, in certain applications it can have significant implications for thermal resistance.