Law for tap water temperature

The Law for Tap Water Temperature: Examining Water Flow Through a Metal Tube

Have you ever wondered what factors affect the temperature of the water coming out of the tap? Specifically, what law describes the rising temperature of the water as it flows through a metal tube connected to a water tank? This article will explore the setup and provide possible solutions.

The Setup

The setup involves a water tank at temperature T, a metal tube of length L connected to it, and a tap at the end where temperature is measured. Water flows through the tube at a rate of P l/s. Initially, the metal tube is at room temperature. Given this setup, we can examine how the temperature of the water changes as it flows through the tube.

The Model

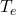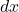To begin with, we need to consider a model where the tube has a constant temperature $T_e$ of length L and radius $r$ . The water is flowing uniformly at a speed $v$ , which can be obtained from the flow P. If we consider a “slice” of water, it will travel an interval $dx$ in a duration of $dt = \frac{dx}{v}$ .

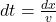The tube will contribute to the heating of the water by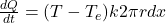 $\frac{dQ}{dt} = (T-T_e) k 2 \pi r dx$ , where 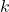$k$ is the conductivity, and where we use a very simple model (in particular, for the radius, we do not distinguish external and internal radii). During this interval, the temperature 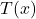$T(x)$ of the water will vary by 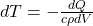$dT = -\frac{dQ}{c \rho dV}$ , where 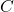$C$ is the heat capacity at constant pressure of water and where $dV = 2 \pi r dx$ .

Replacing these equations, we have $\frac{dT}{T-T_e}=-\frac{k}{\rho C v} dx$ . If the temperature in the tank, i.e. x = 0, is $T_t$ , then the solution is:

where $\alpha = \frac{k}{\rho C v}$ . Depending on the length of the tube, you can determine the temperature at the tap.

Possible Solutions

Now that we have a basic model for our setup, let’s look at possible solutions for the temperature of the water. If we assume that the water flow and the tube conditions are constant, the model can predict the temperature at any point in the tube.

Increasing Temperature

One factor that can affect the temperature of the water is the temperature of the tank. If the tank temperature increases, the temperature of the water in the tube will also increase. Similarly, if the speed of water flow increases, the temperature of the water will increase due to the heat generated from the metal tube. In this scenario, the temperature of water at any point along the tube will increase steadily.

Decreasing Temperature

If there is a decrease in the water tank temperature or a decrease in water flow rate, the temperature of the water in the tube will decrease. The temperature of water at any point along the tube will decrease steadily, and the water temperature at the tap will be lower than what it would have been in the above scenario of increasing temperature.

Steady-State Temperature

If we assume that the temperature of the water tank is constant and the water flow rate is constant, the temperature of the water in the tube will eventually reach a steady-state temperature. In this scenario, over time the temperature will approach a limit temperature, which will remain constant as long as the conditions remain constant. This steady-state temperature is described by the model we have discussed so far.

Maximum Temperature

Another question to explore is what is the maximum temperature of the water that can be achieved in the tube with this setup. In this case, we can see that the maximum temperature of the water is dependent on various factors like conductivity, heat capacity, density, and flow rate. One way to get the maximum temperature is to set the equation $\frac{dT}{dx} = 0$ , and then solve it for x which gives $x = \frac{L}{2}$ . 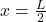Plugging in that value of x into the equation 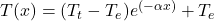$T(x) = (T_t - T_e) e^{(-\alpha x)}+T_e$ , we get the maximum temperature of the water in the tube.

Conclusion

To sum up, the law for the temperature of the water in a metal tube connected to a water tank depends on various factors like tank temperature, water flow rate, the conductivity of the tube, heat capacity of water, and density of water. By using a simple model and some math equations, we can determine the possible solutions and limit temperature of the water.